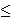 w and G - U is 5-choosable.
w and G - U is 5-choosable.Conjecture 1:
For every surface S there is an integer w such that every
graph G embedded in S has a set U of vertices such that
|U| 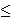 w and G - U is 5-choosable.
w and G - U is 5-choosable.
Conjecture 2: For every surface S there is an integer w such that every graph G embedded in S with edge-width at least w is 5-choosable.
Clearly, Conjecture 2 implies Conjecture 1.
Thomassen [1] proved that graphs on a fixed surface with sufficiently large edge-width are 5-colorable. It is also known that this result cannot be extended to 4-colorings. However, a version of Conjecture 1 for 4-colorings is still open:
Conjecture 3 (Albertson, 1981): For every surface S there is an integer w such that every graph G embedded in S has a set U of vertices such that |U| is at most w and G - U is 4-colorable.
References:
[1] C. Thomassen, Color-critical graphs on a fixed surface, J. Combin. Theory Ser. B 70 (1997) 67-100.
Send comments to Bojan.Mohar@uni-lj.si