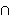Graphs of 4-polytopes

Steinitz proved at the beginning of the 20th century that graphs of (convex) 3-polytopes are precisely the 3-connected planar graphs. However, graphs of 4-polytopes are still a mystery. It is known that they must be 4-connected, but apart from this, not much is known.

Problem 1: Find a good characterization of 4-polytopal graphs.

By a `good' characterization we mean a property that is in NP 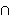co-NP. I believe that this is a very difficult, if not an impossible task. But maybe one can characterize 4-polytopal graphs that satisfy some additional conditions.

Problem 2: Find a good characterization of:

• 5-connected 4-polytopal graphs,
• simplicial 4-polytopal graphs,
• simple (duals of simplicial) 4-polytopal graphs,
• 4-polytopal graphs of girth 4.

Maybe also the above families are difficult to characterize. One may be able to say more if we increase the connectivity or the girth requirement.

Send comments to Bojan.Mohar@uni-lj.si

Revised: februar 17, 2004.